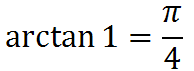カテゴリー: 頭の体操

昔、豊前中津藩の藩主で小笠原長勝という人がいて、延宝元年（1673年）ごろから鬱病にかかったのだそうです。

家臣達はなんとか鬱病を治そうとして上毛郡幸子村に別荘を建て、長勝を住まわせたのですが、長勝は鬱病のわりには贅沢をする意欲は旺盛だったようで、別荘の部屋という部屋に金銀細工を施した他、浴槽は一辺が八間もあるものを作らせ、絶えず湯を張らせていたといいます。さらに、京大阪から名妓を大勢呼んで毎日どんちゃん騒ぎだったそうです。

こういった贅沢のための費用は日に三千貫に及びました。鬱は鬱でもいわゆる新型鬱だったに相違ありません。

さて、当時米一石が五十匁くらいだった（以上、桐畑隆行「豊前歴史風土記」より）そうですが、では三千貫とは米の価格を基準とすると現代だとどのくらいの金額か、が今日の頭の体操です。

—

石（コク）は元来重さの単位ですが、米一石と言う場合は体積を表します。約180.39Lです。これは江戸時代初期から殆ど変わっていません。玄米180.39Lは品質にもよりますが約156kgです。

農水省によると平成26年産米の全銘柄平均価格は玄米60kgあたり12,481円です。

従って米一石の現在の価格は

156 / 60 = 2.6

12481 * 2.6 = 32,450 （円）

です。

上記の書物には五十匁としかありませんが、これは銀五十匁という意味でしょう。銀五十匁は銭四貫文ですから、三千貫は銀五十匁の750倍。つまり、三千貫の価値は

32450 * 750 = 24,337,500 （円）

ということになります。

—

一日2400万円強。かなり粗雑な計算ですが、莫大な費用だったことは確かなようです。

松本清張に「いびき」という短編があって、徳川時代の囚人の様子が書かれています。

牢内では「名主」以下、一番役、二番役、角の隠居、詰の隠居、穴の隠居、三番役、四番役、五番役、頭かぞえ役などの「牢役人」が広い場所に陣取って、ヒラの囚人、平囚は残りの場所にひしめくのだそうです。

そして、牢の広さは間口四間、奥行三間、人数は七十人くらいだったそうですが、この四間×三間とはどのくらいの広さかが、今回の「頭の体操」です。

一間は、およそ 1.818 メートルです。従って、

4 * 3 * 1.818 ^ 2 = 39.661 （m²）

およそ、40 平米ですね。

では、畳にすると何畳でしょう。

畳の大きさには京間、中京間、江戸間がありますが、「いびき」の舞台は江戸（後半は三宅島）なので、江戸間で計算しましょう。

メートルに直さず尺のままの方が簡単です。江戸間では一間は六尺とされています。畳は基本的に長辺が六尺、短辺が三尺ですから、畳一畳は、

6 * 3 = 18 （平方尺）

間口四間、奥行三間の牢内は、

3 * 4 * 6 ^ 2 = 432 （平方尺）

です。従って、

432 / 18 = 24 （畳）

ですね。ただ、実際には京間が「畳割り」といって一畳の面積が不変であるのに比べ、江戸間は「柱割り」といって、柱の分、一畳の寸法は小さくなります。上記の計算はあくまでおおよそです。

それにしても、わずか 二十四 畳の場所に70人、一畳あたり3人とは超過密ですね。それも上述のように牢役人に広い場所を取られた上での話ですから、平囚にとって牢の狭苦しさはさぞや耐え難かったことでしょう。

大金持ちになる方法をご存じでしょうか。まずは以下の問いから入ります。

問い.　紀元1年に1マルクを年利5パーセントで貸した人と、同年から毎年8万マルク稼ぎ続けた人とでは、現在どちらが金持ちになっているか。

まず1マルクを年利5パーセントで貸した人の資産は元本合わせて

1*1.05^2013 = 4.509e+042 （マルク）

ちなみに、4.509掛ける10の42乗は、1京の1京倍よりも大きな数です。

一方、地道に年8万マルク（600万円くらい）稼いでいた人は2013年間飲まず食わずで税金も納めずに貯めても、

80000*2013 = 161040000 （マルク）

にしかなりません。1億6千万マルク。大金には違いありませんが、4.509掛ける10の42乗マルクに比べれば無に等しい金額です。

もうお分かりですね。お金を殖やすには人に貸すことです。地道に稼いでいては殖えません。言い換えれば、給与は算術級数的にしか増えませんが、利子は幾何級数的に増えます。

—

みなさんは言うでしょう、「2000年以上も生きる人はいない」「数字だけ増えても貸した相手に資産がなければ返してもらえない」「年5パーセントは高すぎる」「マルクは廃止された」などなど。

確かにその通りですが、複利というものはある時点から直感に反して急激に増え始めるのは事実です。

恐ろしいのは、マイナスの複利も同じように急激に膨らむということです。つまり、借金は放っておくと取り返しのつかないことになります。

複利の持つ恐るべきパワーに気付いて上手く利用するか、気付かずに人に利用されるかはあなた次第です。

バスにゴルフボールを詰める話をしましたが、少し説明不足だったかもしれません。

この図のように球を同一平面上に三つぴったりくっつけて並べると、それぞれの球の中心を結ぶと正三角形になりますよね。

球の半径が1ならば、正三角形の一辺は2になります。一辺が2の正三角形の高さは√3です。

上の図の横方向は単純に　球の直径 × 球の数　であり、

縦方向は（球の直径を2とすると） 　√3 × 球の数　になっているのがお分かりいただけると思います。

次に上に積んでいく場合です。

このように上に積むと、4つの球の中心を結んだとき正四面体ができますよね。一辺が a の正四面体の高さは、

です。球の半径を r とすると正四面体の一辺の長さは 2r なので、先日書いたように n 個積んだときの高さは

になるわけです。

—

でも、入社試験といった少なからず緊張する場面で上記のような考えをまとめるのは難しそうですね。もっと大ざっぱに、( バスの容積 ÷ ボールの体積 ) × 密度　のような計算法を用いるのも一手です。どのみち、ボールの大きさなどは「勘」ですからね。

最近、入社試験でフェルミ推定をさせるのが流行りだそうです。例えば、バスの中にゴルフボールが何個入るかというような問題です。前提となる数値、この場合バスの容積やゴルフボールの直径などを知っているかということはあまり重視されません。

大事なのは筋道を立てて推測を行うことができるかどうかです。

—

ためしにバスにゴルフボールが何個入るかを推定してみましょう。まず、ボールをざざーっと適当に流し込むか、キッチリ間を詰めて並べるかでアプローチが変わります。どうせ「推定」ですから前者が自然とも言えますが、ここは敢えてキッチリ並べるとして考えます。

上の図をご覧下さい。下の段のボールをきっちり詰めて並べ、そのくぼみに沿うように2段目を並べます。

上から見るとこのようになります。ゴルフボールの半径を r とすると、下の段のボールの中心から上の段のボールの中心までの高さは、

です。従って、n 段並べるとその高さは

です。

さて、フェルミ推定なので、ゴルフボールの直径とバスの容積は調べずに勘で当てなければいけません。私はゴルフボールの直径を4cm、バスの容積を2x2x10で、40立方メートルと考えました。とりあえず、この前提で計算を進めます。

座席などは取っ払ってしまいましょう。とにかく詰め込めるだけ詰め込むのです。

まずは高さについて考えます。ゴルフボールの直径が4cm、つまり半径が2cm、バスの内側の高さが2mなので、

nについて解くと 61.012、切り下げて61個並べられます。奥行きに関しても同様に計算すると288個です。幅（正確には3軸のうち一方向）は単純に4で割る必要があるので、50個です。全部掛け合わせると

61*50*288 = 878,400（個）

ということになります。

座席や、詰め込みが甘く隙間ができてしまうことを考慮すれば、二割減、70万2千7百個くらいでしょうか。

—

後から調べてみると、ゴルフボールの直径は1.68インチ（42.67ミリ）以上だそうで、4cmよりは少し大きいものの案外近かったようです。バスの容積も車種によりますが内側の高さと幅は2.3m前後、奥行きは10m前後のものが多く、私の推定は当たらずとも遠からずだったと言えましょう。

少し前まで PC のスペックを調べる指標として スーパーπ というプログラムがよく使われていました。最近のPCならば数十秒で円周率100万桁まで計算できるはずです。

スーパーπ は計算法もプログラムも高度に洗練されていて素人が真似できるようなものではありませんが、円周率の計算自体はそんなに難しくはありません。

グレゴリ・ライプニッツ級数

よく、プログラミングの初歩で演習課題として与えられるのが、アークタンジェントを無限級数に展開して計算するやり方です。

アークタンジェントは上のような数列（グレゴリ･ライプニッツ級数）で表せます。

なので、1 – 1/3 + 1/5 – 1/7 + 1/9 – … を求めて、4 掛けると π を求めることができます。

ガウス＝ルジャンドルの公式

ちょっと難しいですが素人にもギリギリ理解できて、自分で計算もできそうなのが、ガウス＝ルジャンドルの算術幾何平均を用いた方法です。

この方法は、非常に収束が速く、n桁求めるのに log₂n 回の反復で済みます。スーパーπ もこの方法です。

手元の PC で（Ruby の BigDecimal クラスを使って）素朴にやってみたところ、確かに log₂100 = 6.643、繰り上がって7回の反復で100桁まで正確に計算できました。

しかし、何万桁と求めようとすると恐ろしく時間がかかってしまいます。冒頭にも述べたとおり、円周率を高速に計算するには、かなり高度な数学の知識及びプログラミングの技術が必要です。
ちなみに、Ruby のパッケージにも円周率を求めるサンプルプログラムが入っています。

k, a, b, a1, b1 = 2, 4, 1, 12, 4

while TRUE
  # Next approximation
  p, q, k = k*k, 2*k+1, k+1
  a, b, a1, b1 = a1, b1, p*a+q*a1, p*b+q*b1
  # Print common digits
  d = a / b
  d1 = a1 / b1
  while d == d1
    print d
    $stdout.flush
    a, a1 = 10*(a%b), 10*(a1%b1)
    d, d1 = a/b, a1/b1
  end
end

このプログラムもガウス＝ルジャンドルの公式を使っています。

—

Ruby を使ったもので驚異的なのはほんまの走り書き技術メモで公開されているプログラムで、エレガント且つ圧倒的に高速です。

i7-2600 で、10万桁に1分半かかりません。うーむ、素晴らしい。

 

よく「百歩譲って」と言いますが、この言葉は本来「一歩譲って」だったのがエスカレートして百歩になったものです。「自分としてはこれだけ譲っているんだから」という気持ちを表すために歩数を増やしたのでしょう。

最近では、若い人が「百万歩譲ってもさ～」などと言ったりするのを耳にすることもあります。正直あまり賢く見える言い方ではないので、百歩くらいに留めておいた方が良いとは思いますけどね。

さて、このようにだんだん増える傾向にある「○○歩譲って」ですが、先日なんと「一兆歩譲って……」と言っている人がいました。ハイパーインフレです（笑）

一兆歩って距離にするとどのくらいでしょう。

人間の歩幅は身長の0.45倍ほどだと言います。

1,000,000,000,000 * 1.7 * 0.45 = 765,000,000,000

身長が170cmの人が一兆歩歩くと、約7億6500万kmですね。ちなみに、赤道の長さは約4万77kmですから、

765,000,000 / 40,077 = 19,088

地球を1万9000周する距離です。いくらなんでも譲りすぎですね（笑）

百聞は一見に如かず。次のダイアログをご覧下さい。

複数のモニタを使っている場合、殆どのペンタブレットで、全画面を移動できるようにするか、または一つのモニタの中だけに制限するか選べます。通常は後者を選びます。さもないと、移動できる領域が大変な横長になってしまい、手元の縦横比と画面上の縦横比が異なってしまうからです。仮に全画面を移動でき、且つ縦横比を固定するように設定すると、今度はペンタブ上の利用可能な領域が極端に少なくなってしまいます。

というわけで、領域はプライマリモニタ、縦横比は固定で使うのが常道なのですが、どういうわけか、今朝、全画面且つ縦横比は固定しないという設定（デフォルト）に戻ってしまっていました。

さて、その状態（モニタは二つ、いずれもアスペクト比は16:9、ペンタブは4:3）に於いて、右上から左下へ、45°の角度でペンタブ上に斜線を引くと、画面上では何度になるでしょう？

全画面のアスペクト比は 32:9、ペンタブは4:3、つまり 12:9 ですから、画面の方が 32 / 12 = 2.666…倍、横長です。

まず距離ですが、手元でルート2移動する間に、画面上では

sqrt( 2.666^2 + 1^2 ) = 2.847

移動しますから、

2.847 / 1.414 = 2.013

元より2倍強、長くなってしまいます。

そして、角度は

acos( 1 / 2.847 ) = 69.436 （度）

ですね。

—

まぁ、どうでもいいようなことですね（笑）

ところで、この記事を書いていて 16:9 のペンタブが欲しくなりました。が、近頃散財続きなので今の 4:3 のやつで我慢しようかと思います。