バスにゴルフボールを詰める話をしましたが、少し説明不足だったかもしれません。
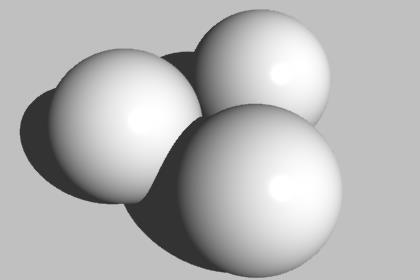
この図のように球を同一平面上に三つぴったりくっつけて並べると、それぞれの球の中心を結ぶと正三角形になりますよね。
球の半径が1ならば、正三角形の一辺は2になります。一辺が2の正三角形の高さは√3です。
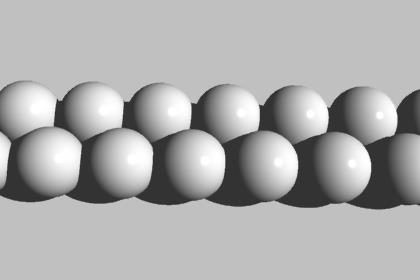
上の図の横方向は単純に 球の直径 × 球の数 であり、
縦方向は(球の直径を2とすると) √3 × 球の数 になっているのがお分かりいただけると思います。
次に上に積んでいく場合です。
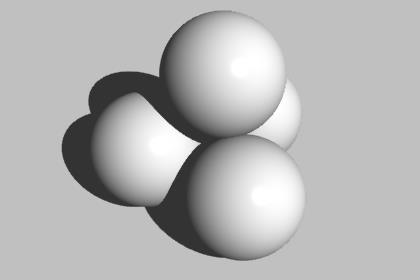
このように上に積むと、4つの球の中心を結んだとき正四面体ができますよね。一辺が a の正四面体の高さは、
![]()
です。球の半径を r とすると正四面体の一辺の長さは 2r なので、先日書いたように n 個積んだときの高さは
![]()
になるわけです。
—
でも、入社試験といった少なからず緊張する場面で上記のような考えをまとめるのは難しそうですね。もっと大ざっぱに、( バスの容積 ÷ ボールの体積 ) × 密度 のような計算法を用いるのも一手です。どのみち、ボールの大きさなどは「勘」ですからね。
