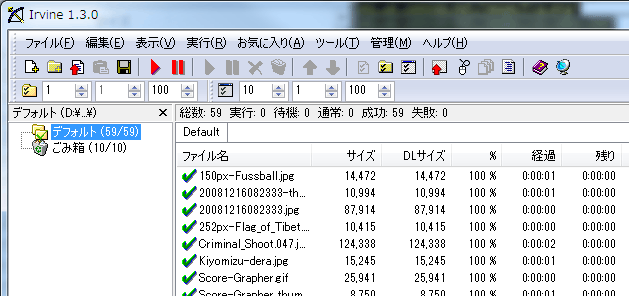
Canvas 3D というライブラリがあります。JavaScript からグラフィックボードの機能を使えてしまうという恐ろしい代物です。これは面白い！ ということで、早速使ってみました。
まだ、デザイン等が未完成ですが、一応プレイできます。ただ、残念ながら IE や Opera には未対応です。今のところ、Google Chrome か Firefox でしか表示できません。
2015年5月16日追記： 現在ではIE 11 でもプレイできます。
※ 「ルービックキューブ」は株式会社メガハウスの登録商標です。
—
今回、幾つか気がついたことを備忘も兼ねて書き記します。
まず、Canvas 3Dでは Collada 形式の3Dモデルを標準としています。例えば、Shade では、10.5 から Collada 形式の出力に対応しましたが、残念ながら私が使っているのは 8.5 で、度重なるアップグレードの奨めもずっとスルーしてきたので、もはやアップグレードパス（2世代前までに限定）がない状態です。
そこで、Metasequoia を使ってモデリング（と言っても、単なる立方体）し、Vixar Motion で読み込んでから、最後に Collada で出力しました。
迂遠且つ若干の制限事項（リンクされた図形が表示されないなど）もありますが、まず Shade で obj 形式で出力し、それをメタセコで読み込み mqo で出力、そして Vixar Motion で Collada へ、というやり方も可能です。
尚、Canvas 3D では、バージョン2.2から立方体などのプリミティブ図形を内部で生成できるようになっています。従って、Collada の必要はなかったとも言えますが、テクスチャ貼りの自由度などの点で、やはり外部ツールでモデリングしてインポートする方が便利です。
クリックされた面の判定
このようなゲーム的なプログラムでは、インタラクティブ性が肝要です。問題はクリックされた面をどうやって判定するかです。
実はC++によるルービックキューブの制作記事を公開されている方がいらっしゃって、大いに参考にさせていただいたのですが、この方の場合、全て自前で描画しているために、非常に高い技術が必要となるかわりに、クリックされた面を知るのは比較的簡単なようなのですね。一方、私の場合、表示はライブラリ任せなので、クリックされた場所がどの面にあたるのかを知る一般的な方法がありません。
仕方がないので、図のようにオブジェクトを（実際には非表示で）配置して、「このオブジェクトがクリックされたらこの面」という具合に判定することにしました。「え？ クリックされたか知る方法はないんじゃなかったの？」と思われるかもしれませんが、違うのです。方法がないのはクリックされた「面」を知ることであって、どのオブジェクトがクリックされたかを知る API はちゃんとあります。面が分からなければ、ユーザーがどの軸に対してどの向きに回転させようとしているのか分からないので、この点は重要です。
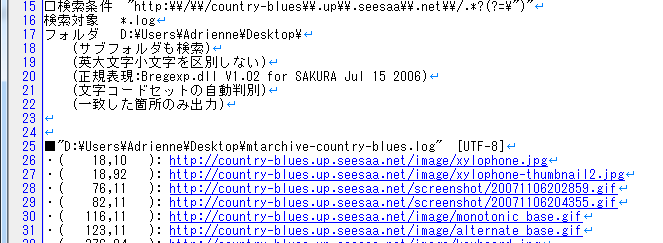
（実はCanvas 3Dでは、最近の仕様変更で非表示のオブジェクトをクリック判定しないようになり、上記の判定法は不可能になりました。各小立方体をさらに面に小分けするなど、対応法は幾つか考えられますが、今回はライブラリのコードをハックして無理やり判定するようにしてしまいました。あまり良い方法ではありません)
6面完成しているかの判定
さて、面の問題が解決すれば、ドラッグによる回転は容易に実装できます。最後に残された問題は、6面完成しているかどうかの判定です。
「各小立方体が最初の位置に戻っていれば6面完成」ではありません。実は完成形には24のパターンがあり、その全てについて判定する必要があります。
サイコロで考えると分かりやすいです。今、1が上を向いています。つまり1の目が出ています。この状態で、4つの側面のどれが正面を向くかで4つのパターンがあることが分かると思います。全ての面について同じことが言えますので、6 * 4 = 24 パターンというわけです。
まあ、理屈は簡単なのですが、実際の判定には全てのパターンの回転行列を求める必要があります。手計算ではとてもやってられないので、Ruby の行列演算を使いました。例えば、次のような感じです。
require 'matrix'
y = -Math::PI/2
z = Math::PI
cos_y = Math.cos(y)
sin_y = Math.sin(y)
cos_z = Math.cos(z)
sin_z = Math.sin(z)
m1 = Matrix[[cos_y,0,sin_y,0],[0,1,0,0],[-sin_y,0,cos_y,0],[0,0,0,1]]
m2 = Matrix[[cos_z,-sin_z,0,0],[sin_z,cos_z,0,0],[0,0,1,0],[0,0,0,1]]
p m2 * m1
Y軸を中心に-90度、Z軸を中心に180度回転させる場合の回転行列を求めています。cos(-90)は 0、sin(-90) は-1、cos(180)は-1、sin(180)は0、と言う風に、0 や 1 が並びますから、そんなに難しい計算ではありませんが、手計算で24パターンもやるのは上述の通りかなり大変です。
こうやって求めた回転行列を使った、六面完成チェック関数が以下です。
function check(){
var ok;
var pos;
var mat = [];
mat[0] = [1 ,0 ,0 ,0 ,0 ,1 ,0 ,0 ,0 ,0 ,1 ,0 ,0 ,0 ,0 ,1];
mat[1] = [1 ,0 ,0 ,0 ,0 ,0 ,1 ,0 ,0,-1 ,0 ,0 ,0 ,0 ,0 ,1];
mat[2] = [1 ,0 ,0 ,0 ,0,-1 ,0 ,0 ,0 ,0,-1 ,0 ,0 ,0 ,0 ,1];
mat[3] = [1 ,0 ,0 ,0 ,0 ,0,-1 ,0 ,0 ,1 ,0 ,0 ,0 ,0 ,0 ,1];
mat[4] = [0,-1 ,0 ,0 ,1 ,0 ,0 ,0 ,0 ,0 ,1 ,0 ,0 ,0 ,0 ,1];
mat[5] = [0,-1 ,0 ,0 ,0 ,0,-1 ,0 ,1 ,0 ,0 ,0 ,0 ,0 ,0 ,1];
mat[6] = [0 ,1 ,0 ,0 ,1 ,0 ,0 ,0 ,0 ,0,-1 ,0 ,0 ,0 ,0 ,1];
mat[7] = [0 ,0 ,1 ,0 ,1 ,0 ,0 ,0 ,0 ,1 ,0 ,0 ,0 ,0 ,0 ,1];
mat[8] = [0 ,1 ,0 ,0,-1 ,0 ,0 ,0 ,0 ,0 ,1 ,0 ,0 ,0 ,0 ,1];
mat[9] = [0 ,0 ,1 ,0,-1 ,0 ,0 ,0 ,0,-1 ,0 ,0 ,0 ,0 ,0 ,1];
mat[10] = [0,-1 ,0 ,0,-1 ,0 ,0 ,0 ,0 ,0,-1 ,0 ,0 ,0 ,0 ,1];
mat[11] = [0 ,0,-1 ,0,-1 ,0 ,0 ,0 ,0 ,1 ,0 ,0 ,0 ,0 ,0 ,1];
mat[12] = [-1 ,0 ,0 ,0 ,0,-1 ,0 ,0 ,0 ,0 ,1 ,0 ,0 ,0 ,0 ,1];
mat[13] = [-1 ,0 ,0 ,0 ,0 ,0,-1 ,0 ,0,-1 ,0 ,0 ,0 ,0 ,0 ,1];
mat[14] = [-1 ,0 ,0 ,0 ,0 ,1 ,0 ,0 ,0 ,0,-1 ,0 ,0 ,0 ,0 ,1];
mat[15] = [-1 ,0 ,0 ,0 ,0 ,0 ,1 ,0 ,0 ,1 ,0 ,0 ,0 ,0 ,0 ,1];
mat[16] = [0 ,0,-1 ,0 ,0 ,1 ,0 ,0 ,1 ,0 ,0 ,0 ,0 ,0 ,0 ,1];
mat[17] = [0 ,1 ,0 ,0 ,0 ,0 ,1 ,0 ,1 ,0 ,0 ,0 ,0 ,0 ,0 ,1];
mat[18] = [0 ,0,-1 ,0 ,1 ,0 ,0 ,0 ,0,-1 ,0 ,0 ,0 ,0 ,0 ,1];
mat[19] = [0 ,0 ,1 ,0 ,0,-1 ,0 ,0 ,1 ,0 ,0 ,0 ,0 ,0 ,0 ,1];
mat[20] = [0 ,0 ,1 ,0 ,0 ,1 ,0 ,0,-1 ,0 ,0 ,0 ,0 ,0 ,0 ,1];
mat[21] = [0,-1 ,0 ,0 ,0 ,0 ,1 ,0,-1 ,0 ,0 ,0 ,0 ,0 ,0 ,1];
mat[22] = [0 ,0,-1 ,0 ,0,-1 ,0 ,0,-1 ,0 ,0 ,0 ,0 ,0 ,0 ,1];
mat[23] = [0 ,1 ,0 ,0 ,0 ,0,-1 ,0,-1 ,0 ,0 ,0 ,0 ,0 ,0 ,1];
for( var m=0; m<24; m++ ){
ok = true;
loop:for( var i=0; i<3; i++ ){
for( var j=0; j<3; j++ ){
for( var k=0; k<3; k++ ){
pos = c3dl.multiplyMatrixByVector( mat[m], things[i][j][k].getPosition() );
if( pos[0] != (i-1)*20 || pos[1] != (j-1)*20 || pos[2] != (k-1)*20 ){
ok = false;
break loop;
}
}
}
}
if( ok ){
break;
}
}
return ok;
}
0 と 1 がこれでもかと並んでますね（笑）
ちなみに、mat[0]はなにも回転しない場合で、本来必要ありませんが、美観のために入れてあります（笑）
ご覧のように Canvas 3D にも行列演算を行ってくれるユーティリティー(c3dl.multiplyMatrixByVector())があります。こちらは、Rubyと少し使い方が違って、要素数16の配列を渡すと、4行4列の行列として扱ってくれます。
WebGLは普及するか
Canvas 3Dは WebGLという技術を使用しており、この WebGL は、ネイティブアプリには劣るものの、グラフィックボードの機能を利用した、かなり本格的な3D表現が可能です。
今回使ってみた感触では、少なくともメタセコで作ったモデルを表示するまでは非常に簡単でした。「これならいくらでもゲーム作れるじゃん！」と、思わずドメインまで取ってしまいました（ webglgame.jp ）。
ところが、Microsoft は、自社の DirectX を推進する目的もあってか WebGL に反対していて、現在はもちろん、将来にわたって IE でのサポートは絶望的なようです。
折角の有望な技術が、最大シェアのブラウザでサポートされないばかりに廃れてしまうとしたら惜しいことです。幸い（？）、Google Chrome などのより先進的なブラウザに乗り換える人が増えていますので、この流れが加速することを祈るばかりです。
Opera や Safari でも、もうじき対応するとのことです。
関連記事：Canvas3D によるルービックキューブ、そして日本の教育について
画像をクリックすると拡大表示してくれる FancyBox という WordPress プラグインを導入しました。
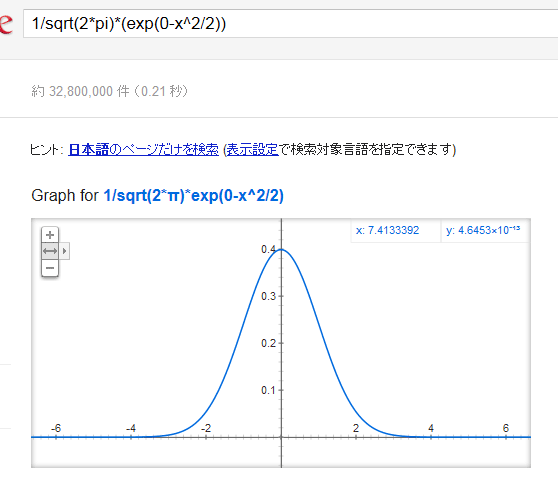
図をご覧下さい。細い矢印がX軸、太い矢印がドラッグ方向です。キューブの中心に原点があります。X軸は（3次元の）単位ベクトルで表すと(1,0,0)です。これを2次元に投射すると、カメラの位置によって様々な値を取り得るのですが、今回はその計算は省略して、とりあえず、図のように下向き45°で表示されているとしましょう。この場合、1/sqrt(2) = 0.707 ですから、X軸のベクトルは2次元で表すと(0.707, -0.707)です。
