今日はちょっとした頭の体操です。
今、CD アルバムの中に 16 曲入っているとします。その中でお気に入りはただ一曲です。ランダム(シャッフルではなく)に曲をかけていって、16 曲以内にその曲がかかる確率は?
実は答えは計算しなくても分かります。約 63% になるはずです。以下に簡単に説明します。
まず、1 回の試行でその曲がかかる確率 p は当然 1/16 ですね。これは簡単。
では、16 回やって 16 回ともかからない確率 y はどうでしょう。
y = ( 1 – p ) ^ ( 1 / p )
= ( 1 – 1/16 ) ^ ( 1 / (1/16) )
= 0.356
従って、16 回のうち 1 回でもかかる確率は 1 – 0.356 = 0.644
あれ、1% 誤差が出てしまいました。が、事前の予測は概ね正確でした。
なぜ分かるのかと言いますと、ある事象の起きる確率が p のとき、 1/p 回試行して一度もその事象が起きない確率 y は、p が十分小さければ自然対数の底 e の逆数に近似するからです。
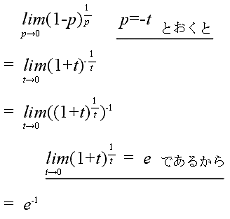
つまり、上記の例で言いますと、16 曲だろうと 100 曲だろうと、確率分母の回だけかけて少なくとも一度はお気に入りの曲がかかる確率は 1 – e-1 = 0.632
常に、約 63% になります。理屈は少々難しいですが、使い方は驚くほど簡単です。それにしても、e の性質は本当に不思議ですね。
さてさて、お正月から随分と頭を使ってしまいました。頭を休めるために Furry Lewis でも聴こうと思います。Back On My Feet Again はいつかかるかな~。
