π > 3.05 の証明

確認していませんが、聞くところによると、最近の東大の入試で「円周率が 3.05 より大きいことを証明せよ」というのが出たそうです。

なかなか面白い問題です。

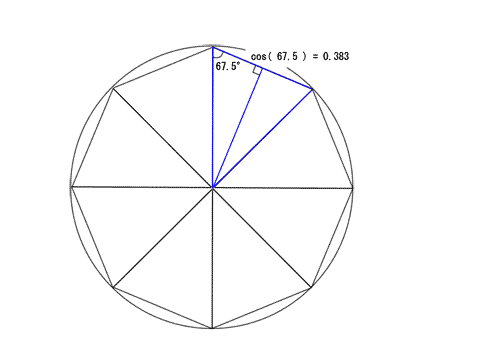
私は、上のような図を頭の中に作って、正八角形の中の八つの二等辺三角形の相等しい角が 67.5°なので、円の直径を 1 とすると、円に内接する正八角形の一辺は、

cos( 67.5 ) = 0.383

従って、正八角形の外周は、

0.383 * 8 = 3.064

円周は正八角形の外周より明らかに大きいので、円周率は 3.05 より大きい。

……というふうにやってみたのですが、この方法の泣き所は cos( 67.5 ) を計算しなくてはいけないことですね。

試験場では関数電卓は使えないでしょうし……。

受験生のみなさんはどうやって解いたのでしょうね。上手い方法をご存じの方はぜひ教えて下さい。