ガウス＝ルジャンドルの算術幾何平均を用いた円周率の計算法

少し前まで PC のスペックを調べる指標として スーパーπ というプログラムがよく使われていました。最近のPCならば数十秒で円周率100万桁まで計算できるはずです。

スーパーπ は計算法もプログラムも高度に洗練されていて素人が真似できるようなものではありませんが、円周率の計算自体はそんなに難しくはありません。

グレゴリ・ライプニッツ級数

よく、プログラミングの初歩で演習課題として与えられるのが、アークタンジェントを無限級数に展開して計算するやり方です。

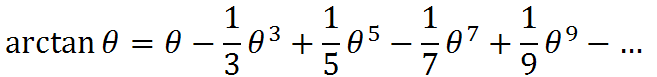
アークタンジェントは上のような数列（グレゴリ･ライプニッツ級数）で表せます。

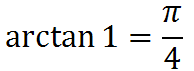
なので、1 – 1/3 + 1/5 – 1/7 + 1/9 – … を求めて、4 掛けると π を求めることができます。

ガウス＝ルジャンドルの公式

ちょっと難しいですが素人にもギリギリ理解できて、自分で計算もできそうなのが、ガウス＝ルジャンドルの算術幾何平均を用いた方法です。

この方法は、非常に収束が速く、n桁求めるのに log₂n 回の反復で済みます。スーパーπ もこの方法です。

手元の PC で（Ruby の BigDecimal クラスを使って）素朴にやってみたところ、確かに log₂100 = 6.643、繰り上がって7回の反復で100桁まで正確に計算できました。

しかし、何万桁と求めようとすると恐ろしく時間がかかってしまいます。冒頭にも述べたとおり、円周率を高速に計算するには、かなり高度な数学の知識及びプログラミングの技術が必要です。
ちなみに、Ruby のパッケージにも円周率を求めるサンプルプログラムが入っています。

k, a, b, a1, b1 = 2, 4, 1, 12, 4

while TRUE
  # Next approximation
  p, q, k = k*k, 2*k+1, k+1
  a, b, a1, b1 = a1, b1, p*a+q*a1, p*b+q*b1
  # Print common digits
  d = a / b
  d1 = a1 / b1
  while d == d1
    print d
    $stdout.flush
    a, a1 = 10*(a%b), 10*(a1%b1)
    d, d1 = a/b, a1/b1
  end
end

このプログラムもガウス＝ルジャンドルの公式を使っています。

—

Ruby を使ったもので驚異的なのはほんまの走り書き技術メモで公開されているプログラムで、エレガント且つ圧倒的に高速です。

i7-2600 で、10万桁に1分半かかりません。うーむ、素晴らしい。