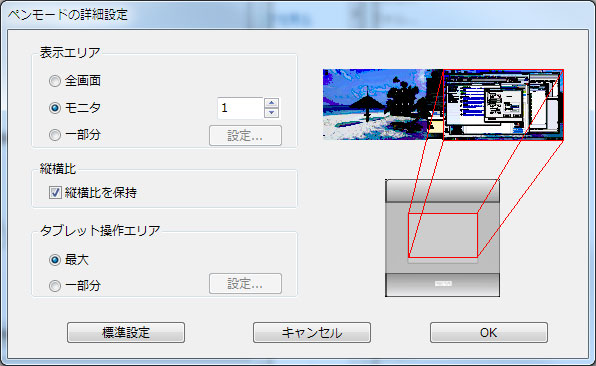
百聞は一見に如かず。次のダイアログをご覧下さい。
複数のモニタを使っている場合、殆どのペンタブレットで、全画面を移動できるようにするか、または一つのモニタの中だけに制限するか選べます。通常は後者を選びます。さもないと、移動できる領域が大変な横長になってしまい、手元の縦横比と画面上の縦横比が異なってしまうからです。仮に全画面を移動でき、且つ縦横比を固定するように設定すると、今度はペンタブ上の利用可能な領域が極端に少なくなってしまいます。
というわけで、領域はプライマリモニタ、縦横比は固定で使うのが常道なのですが、どういうわけか、今朝、全画面且つ縦横比は固定しないという設定(デフォルト)に戻ってしまっていました。
さて、その状態(モニタは二つ、いずれもアスペクト比は16:9、ペンタブは4:3)に於いて、右上から左下へ、45°の角度でペンタブ上に斜線を引くと、画面上では何度になるでしょう?
全画面のアスペクト比は 32:9、ペンタブは4:3、つまり 12:9 ですから、画面の方が 32 / 12 = 2.666…倍、横長です。
まず距離ですが、手元でルート2移動する間に、画面上では
sqrt( 2.666^2 + 1^2 ) = 2.847
移動しますから、
2.847 / 1.414 = 2.013
元より2倍強、長くなってしまいます。
そして、角度は
acos( 1 / 2.847 ) = 69.436 (度)
ですね。
—
まぁ、どうでもいいようなことですね(笑)
ところで、この記事を書いていて 16:9 のペンタブが欲しくなりました。が、近頃散財続きなので今の 4:3 のやつで我慢しようかと思います。